Todo sobre Estructuras

 

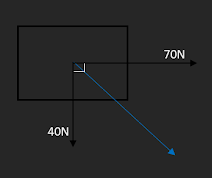
 Sistema de Fuerzas Fuerza resultante del siguiente sistema de fuerza       Primera ley de Newton: Todo cuerpo permanecerá en reposo o movimiento constante siempre y cuando no exista una fuerza externa que le obligue cambiar de estado.      Dicho esto empezaremos con un ejercicio para poder dar a entender más la teoría de Newton explicada anteriormente.      Empezando con que tenemos dos tipos de fuerza: Fuerza concurrente: son las fuerzas que se aplican sobre un mismo punto, y Fuerza no concurrente: con las fuerzas que se aplican sobre distintos puntos de un cuerpo rígido.      Para empezar este cálculo debemos tomar en cuenta que vamos a utilizar el teorema de pitágoras con la fórmula (a²+b²=c²) y las leyes de senos y cosenos. a²+b²=c²  =  70² + 40² = FR²  =  FR= 80.62N      Ya como elemento final buscaremos encontrar el ángulo interno con la ley de senos y cosenos.   ...

Magnitud de la fuerza "F" y el ángulo "Θ"      Para empezar este ejercicio tomaremos en cuenta dos fórmulas: ∑ Fx= F cos ∝ Fy= F sen ∝      Empezaremos ahora primero sacando el sen ∝= sen∝ 12/13 ∝= 67.38°      Con este dato utilizaremos la fórmula Fx= F cos∝ reemplazando con los datos que tenemos: Fx= 325 cos67.38= 125N Fx= 325(5/13) = 125N ➙ Fy= 325(12/13)= 300N↑ Fx= 600 cos45°= 424.26N→ Fy= 600 sen45°= 424.26N↓ Fx= Fcos⦵→ Fy= Fsen⦵↑ +  ∑Fx= 125 + 424. 25 + Fcos⦵=0 →  = 125 + 424.25 + Fcos⦵=0     =    Fcos⦵=-549.26    =     F=-549.26/cos⦵ +↑∑Fy= 300 - 424.26 + Fsen⦵=0       = 300 - 424.26 + Fsen⦵= 0     =     Fsen⦵= 124.26     =    F=124.26/sen⦵ -549.26  =  124.26        =            sen⦵  =  124.26 cos⦵     =   sen⦵      ...

  Momento de una Fuerza      Cuando una fuerza se aplica a un cuerpo, esta; produce una tendencia a que el cuerpo rote alrededor de un punto que no está en la línea de acción de la fuerza.      Magnitud: producto de la fuerza por la distancia perpendicular hacia el punto de referencia. (M= F x D)      Es conveniente que aunque no indispensable que la dirección del momento en sentido contrario a las manecillas del reloj, se considere positivo y en sentido de las manecillas sea negativo. ⤿+      -⤾      Momento resultante: puede determinarse al encontrar la suma algebraica de los momentos causados por todas las fuerzas del sistema, es decir:      EM͎ . = MR= F1d1 + F2d2 + Fndn      a=0      EM . = 0       EFx=0           EFy=0

 Tipos de Apoyos      Vigas Isostáticas: Son las vigas que tienen un solo apoyo      Vigas Hiperestáticas: Son las que tienen 2 tipos de apoyo. -Empotrado -Simple/fijo -Rodillo -Articulado    Ejemplo de cálculos de momento:      MRA= -200 (2) - 400 (5) = 400 - 2000= -2400 N.m      En este caso para calcular el momento de “A” todos los momentos van en sentido de las manecillas del reloj (↻), ya que de acuerdo a su teoría en estos casos se tomaron todos con signo negativo (-), completando así la fórmula del momento en negativo (-)      MRB= 200(6) + 400(2)= 1200 + 1200= 2400 N.m      Ahora para poder calcular el momento de “B” todos los momentos van en el sentido contra las manecillas del reloj (↺), esto produce que de acuerdo a la teoría todos los números se contarán en positivo (+), completando así la fórmula del momento en positivo (+).

 Cálculo de Reacciones     Para calcular las diferentes reacciones en una viga es necesario primero tener en cuenta estas tres fórmulas: ΣFx=0 ΣFy=0 ΣMo=0     En este caso analizaremos una viga que contiene momentos y cargas puntuales. P1=5kN P2=2kN P3=7kN M1=6kN*m M2=12kN*m M3=7kN*m M4=4kN*m      Primero se tiene que localizar un apoyo en el cual nos vamos a basar, en este caso será A. Una vez dicho el punto de inicio empezaremos por ver con cual fórmula se empezará, analizando la viga vemos que no tenemos fuerzas en X, pero tenemos momentos y cargas en Y. Entonces al ver la viga vemos que no podemos solo usar las fuerzas en Y debido a que no conocemos ninguna de las reacciones por lo tanto usaremos la fórmula de los momentos (ΣMo=0). Para sacar los momentos de las cargas puntuales se debe multiplicar fuerza(F) por distancia (d).     El cáalculo quedaría de esta manera: →+ΣMA= 2(3)+4-12-5(5)-6+RB(11)-7(13)-7=0 →+ΣMA= 6+4-12-25-6+RB(11)-...

 Análisis de Cargas Continuas      Una carga continua se analizará como una carga puntual, ubicandola en su centroide. Para ello pondremos un ejemplo de una viga para explicar. P1= 5kN P2= 7kN W1= 5kN/m M1= 6kN*m      Como primer paso es necesario determinar el centroide de la carga continua, en este caso la distancia es de 6m por lo tanto se tomará en cuenta como 3m de distancia y para su carga se deberá multiplicar la fuerza (kN) por la distancia (m) para su cálculo de momento, dicho esto se hace una sumatoria de momentos para determinar cualquier reacción, en este caso tomaremos A como incógnita.     La operación quedaría de esta manera: →+ΣMA= 5(1)-30(6)-6+RB(12)-7(14)=0 →+ΣMA= 5-180-6-98+RB(12)=0 →+ΣMA= -279+RB(12)=0 →+ΣMA= RB(12)=279 →+ΣMA= RB=279/12 →+ΣMA= RB=23.25kN     Con este resultado sabemos la reacción en B entonces para sacar la reacción en A solo hacemos una sumatoria de fuerzas en Y (ΣFy). ↑+ΣFy= -5+RA-30+RB-7=0 ↑+Σ...

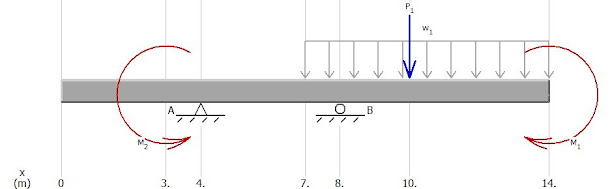
  Diagrama de Cortante      Diagrama de cortante (V):  sirve para saber los puntos donde una viga puede sufrir un esfuerzo al corte y se obtiene mediante las cargas verticales, reacciones y longitudes de ellas; a las que se encuentran.      Generalidades: Una carga puntual o punto de apoyo origina una linea vertical.  Una carga uniforme rectangular origina una linea inclinada. Las regiones donde no hay cargas se reflejan como linea horizontal. Una carga continua no uniforme (triangular) origina una arco de parabola. El diagrama se traza en un plano; hacia arriba (+) y hacia abajo (-). Viga de Ejemplo Diagrama de Cortante (V)

 Diagrama de Momento           Diagrama de momento (M):  Este diagrama nos indica los esfuerzo flexionantes que sufrira la viga.      Generalidades: Un momento externo aplicado en un punto de la viga, origina una linea Una linea horizontal en el diagrama cortante implica una linea inclinada en el diagrama de momento. Una linea inclinada en el diagrama de cortante implica una arco de parabola en el diagrama de momento. (si la pendiente es hacia abajo; la parabola es concava hacia arriba y viceversa). El diagrama se trazara mediante las areas del diagrama de cortante y en sentido inverso. Diagrama de Cortante (V) Diagrama de Momento (M)

  Diseño de Perfiles     Para el cálculo de Zx que es utilizado para determinar el tipo de viga que se usará es necesario primero conocer la Capacidad de Carga Admisible (qadm), este valor depende de si la viga es de acero contínuo o es acero con perforaciones, y el Momento Máximo (Mu), además es necesario tener la fuerza que se le va a aplicar (Fy), con esto podemos determinar Zx con la siguiente fórmula: Zx=Mu/qadm(Fy).     Una vez determinado el valor de Zx se consulta la tabla de perfiles de las cuales se hacen propuestas de acuerdo a este mismo valor. tablas Perfiles-CIRSOC (yumpu.com)