Todo sobre Estructuras

  ARMADURAS       Las armaduras son estructuras compuestas de elementos esbeltos unidos entre sí en sus puntos extremos. A estos elementos esbeltos se les llama “barras” y a los puntos de unión se les conoce como “nodos”.  Las armaduras se utilizan para la construcción de estructuras de grandes longitudes, como: puentes, torres, techumbres, grúas, etc.         Ahora bien, dentro de las fuerzas que se le pueden aplicar a un nodo, estas determinarán si el nodo está a presión o compresión, y una de las formas más básicas de comprender esto es cuando la fuerza total quede en números positivos (+) esta será un momento de tensión, cuando en su contrario una vez que el resultado sea negativo (-) esta será a compresión.

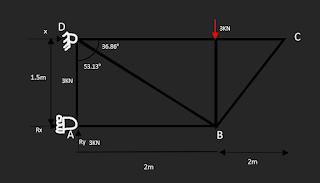
  Método de nodos      El método de los nodos o método de los nudos, consiste en el planteamiento de equilibrio mecánico de cada uno de los nodos o nudos de una armadura simple. Un nodo es cada uno de los puntos donde concurren dos o más barras. El equilibrio global de la estructura implica que el equilibrio local de cada uno de los nodos. Se resuelve de la siguiente manera: Tan= c.o/c.a= 1.5/2= 36.86° 90° - 36.86°= 53.13 ⤿+⅀M A = Ry (2) - 3(2)             = Ry (2) - 6 = 0            = Ry= 6/2= -3 (compresión) -↑⅀Fy B = 3KN + BD sen 53.13= 0               BD= -3KN/sen 53.13= -3.75KN (compresión) →⅀Fx= AB - BD cos 36.86= 0             AB= 3.0KN (tension) ↑⅀Fy= AD - BD sen 53.13= 0        ...

Método de Secciones      El método de las secciones se usa para determinar las cargas que actúan dentro de un cuerpo. Se basa en el principio de que, si un cuerpo está en equilibrio, entonces cualquier parte del cuerpo está también en equilibrio. Problema.  Calcula las fuerzas en las barras AC, BC, BD del problema anterior, usando ahora el método de las secciones 1. Solución 1.1 Reacciones en los apoyos Primero analizamos la estructura como un todo para calcular las reacciones en los apoyos. La ligadura en el punto  A  es una articulación, por lo que la fuerza puede tener dos componentes. La ligadura en el punto  E  es un apoyo en rodillo, esto es, la reacción sólo puede tener componente perpendicular al suelo. Expresamos las posibles componentes de las reaccione y sus momentos respecto del punto  A  en sistema de ejes indicado en la figura Expresamos las cargas y sus momentos respecto al punto  A  usando el sistema de ejes ind...

 

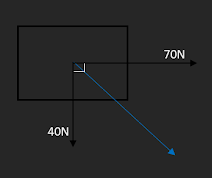
 Sistema de Fuerzas Fuerza resultante del siguiente sistema de fuerza       Primera ley de Newton: Todo cuerpo permanecerá en reposo o movimiento constante siempre y cuando no exista una fuerza externa que le obligue cambiar de estado.      Dicho esto empezaremos con un ejercicio para poder dar a entender más la teoría de Newton explicada anteriormente.      Empezando con que tenemos dos tipos de fuerza: Fuerza concurrente: son las fuerzas que se aplican sobre un mismo punto, y Fuerza no concurrente: con las fuerzas que se aplican sobre distintos puntos de un cuerpo rígido.      Para empezar este cálculo debemos tomar en cuenta que vamos a utilizar el teorema de pitágoras con la fórmula (a²+b²=c²) y las leyes de senos y cosenos. a²+b²=c²  =  70² + 40² = FR²  =  FR= 80.62N      Ya como elemento final buscaremos encontrar el ángulo interno con la ley de senos y cosenos.   ...

Magnitud de la fuerza "F" y el ángulo "Θ"      Para empezar este ejercicio tomaremos en cuenta dos fórmulas: ∑ Fx= F cos ∝ Fy= F sen ∝      Empezaremos ahora primero sacando el sen ∝= sen∝ 12/13 ∝= 67.38°      Con este dato utilizaremos la fórmula Fx= F cos∝ reemplazando con los datos que tenemos: Fx= 325 cos67.38= 125N Fx= 325(5/13) = 125N ➙ Fy= 325(12/13)= 300N↑ Fx= 600 cos45°= 424.26N→ Fy= 600 sen45°= 424.26N↓ Fx= Fcos⦵→ Fy= Fsen⦵↑ +  ∑Fx= 125 + 424. 25 + Fcos⦵=0 →  = 125 + 424.25 + Fcos⦵=0     =    Fcos⦵=-549.26    =     F=-549.26/cos⦵ +↑∑Fy= 300 - 424.26 + Fsen⦵=0       = 300 - 424.26 + Fsen⦵= 0     =     Fsen⦵= 124.26     =    F=124.26/sen⦵ -549.26  =  124.26        =            sen⦵  =  124.26 cos⦵     =   sen⦵      ...